내적과 외적

내적 | 內積 | inner product

적은 쌓는다는 뜻의 한자, 여기서는 곱한다는 뜻

벡터의 곱하기는 2가지 정의가 있는데, 내적은 벡터를 마치 수처럼 곱하는 개념

 

벡터에는 방향이 있으므로, 방향이 일치하는 만큼 곱한다.

예를 들어 두 벡터의 방향이 같으면, 두 벡터의 크기를 그냥 곱한다.

 

두 벡터가 이루는 각이 90도일 땐, 일치하는 정도가 전혀 없기 때문에 내적의 값은 0이다.

내적은 한 벡터를 다른 벡터로 정사영 시켜서, 그 벡터의 크기를 곱한다.

 

외적 | 外積 | outer product

두 벡터를 곱하는 또다른 정의로 외적이 있다. 외적의 결과값은 벡터인데, 방향은 곱하는 두 벡터에 수박하고, 크기는 두 벡터가 이루는 정사각형의 넓이이다. 외적의 연산 기호는 크로스이다. (u→×v→) 외적의 크기(절대값)만 나타내보면, 다음과 같다.

 

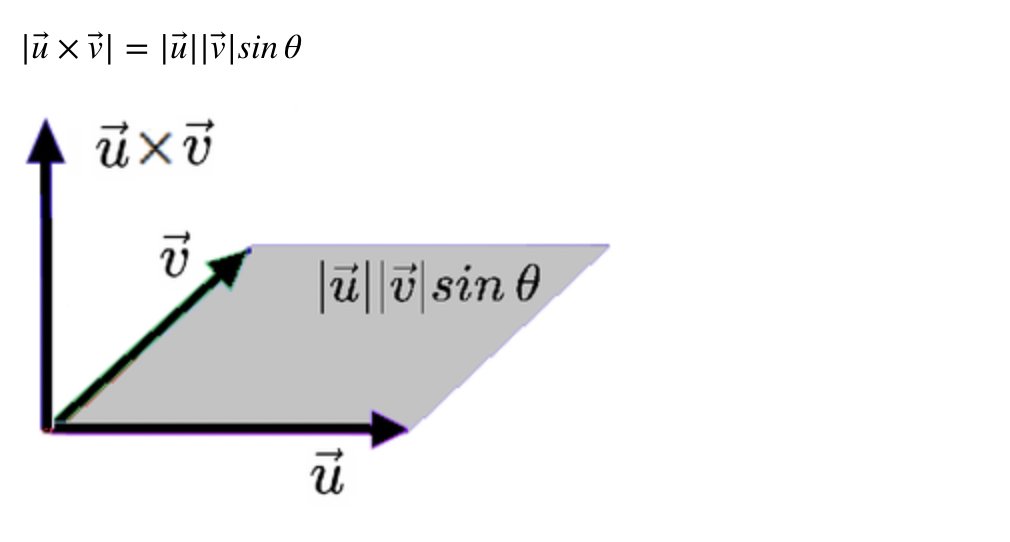
내적과 외적은 서로 상관이 없다. 

두 가지 형태의 다른 연산이 존재하는 것이다.

 

내적의 결과값은 스칼라이고, 외적의 결과값은 벡터이다.